| (x, y) | P(X = x, Y = y) |
|---|---|
| (2, 1) | 0.0625 |
| (3, 2) | 0.1250 |
| (4, 2) | 0.0625 |
| (4, 3) | 0.1250 |
| (5, 3) | 0.1250 |
| (5, 4) | 0.1250 |
| (6, 3) | 0.0625 |
| (6, 4) | 0.1250 |
| (7, 4) | 0.1250 |
| (8, 4) | 0.0625 |
12 Joint Distributions
Example 12.1 Roll a fair four-sided die twice. Let \(X\) be the sum of the two dice, and let \(Y\) be the larger of the two rolls (or the common value if both rolls are the same). Recall Table 5.1.
- Compute and interpret \(p_{X, Y}(5, 3) = \text{P}(X = 5, Y = 3)\).
- Construct a “flat” table displaying the distribution of \((X, Y)\) pairs, with one pair in each row.
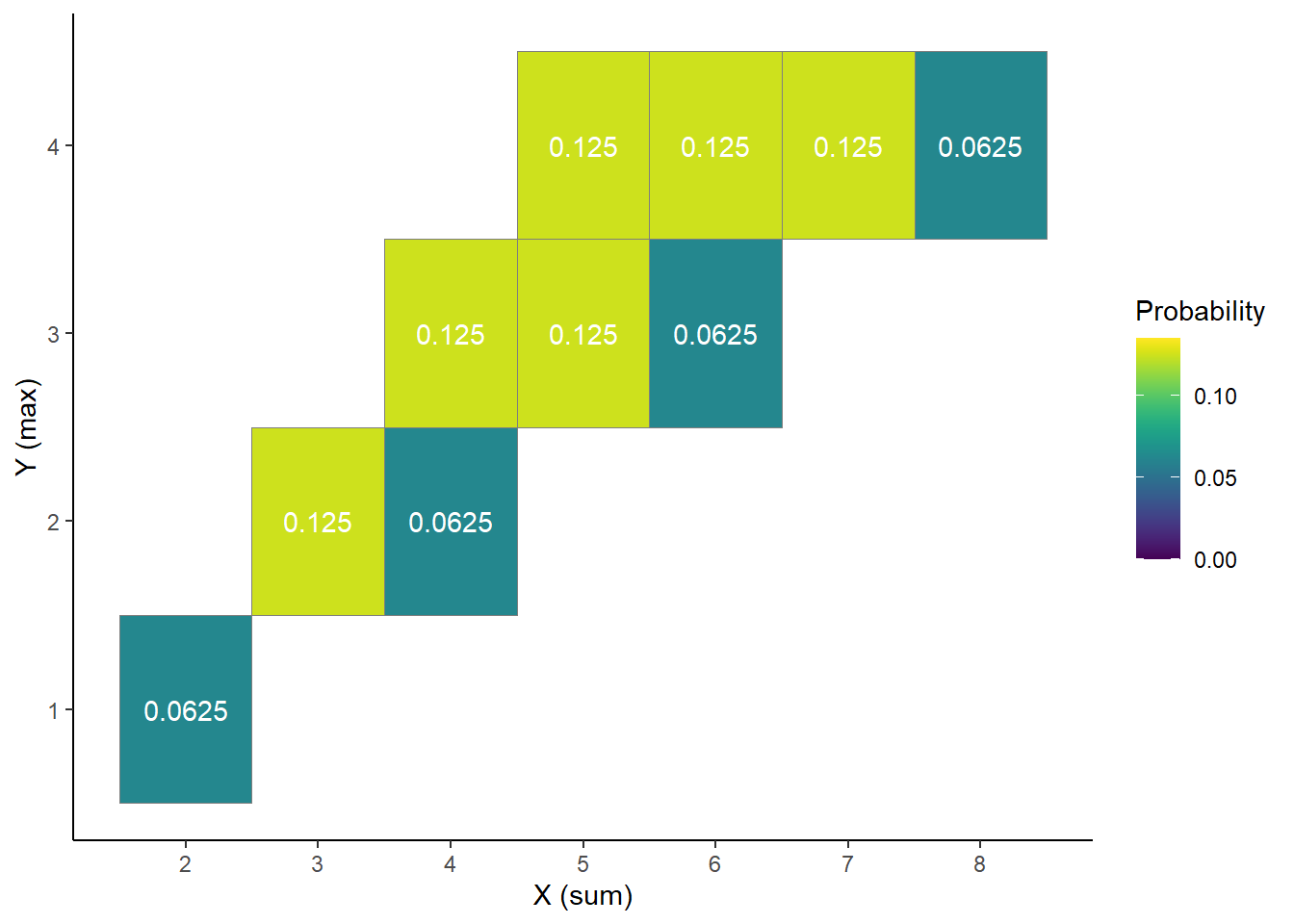
- Construct a two-way displaying the joint distribution on \(X\) and \(Y\).
- Sketch a plot depicting the joint distribution of \(X\) and \(Y\).
- Starting with the two-way table, how could you obtain \(\text{P}(X = 5)\)?
- Starting with the two-way table, how could you obtain the marginal distribution of \(X\)? of \(Y\)?
- Starting with the marginal distribution of \(X\) and the marginal distribution of \(Y\), could you necessarily construct the two-way table of the joint distribution? Explain.
- The joint distribution of random variables \(X\) and \(Y\) is a probability distribution on \((x, y)\) pairs, and describes how the values of \(X\) and \(Y\) vary together or jointly.
- Marginal distributions can be obtained from a joint distribution by “stacking”/“collapsing”/“aggregating” out the other variable.
- In general, marginal distributions alone are not enough to determine a joint distribution. (The exception is when random variables are independent.)
| \(x\) \ \(y\) | 1 | 2 | 3 | 4 |
| 2 | 1/16 | 0 | 0 | 0 |
| 3 | 0 | 2/16 | 0 | 0 |
| 4 | 0 | 1/16 | 2/16 | 0 |
| 5 | 0 | 0 | 2/16 | 2/16 |
| 6 | 0 | 0 | 1/16 | 2/16 |
| 7 | 0 | 0 | 0 | 2/16 |
| 8 | 0 | 0 | 0 | 1/16 |
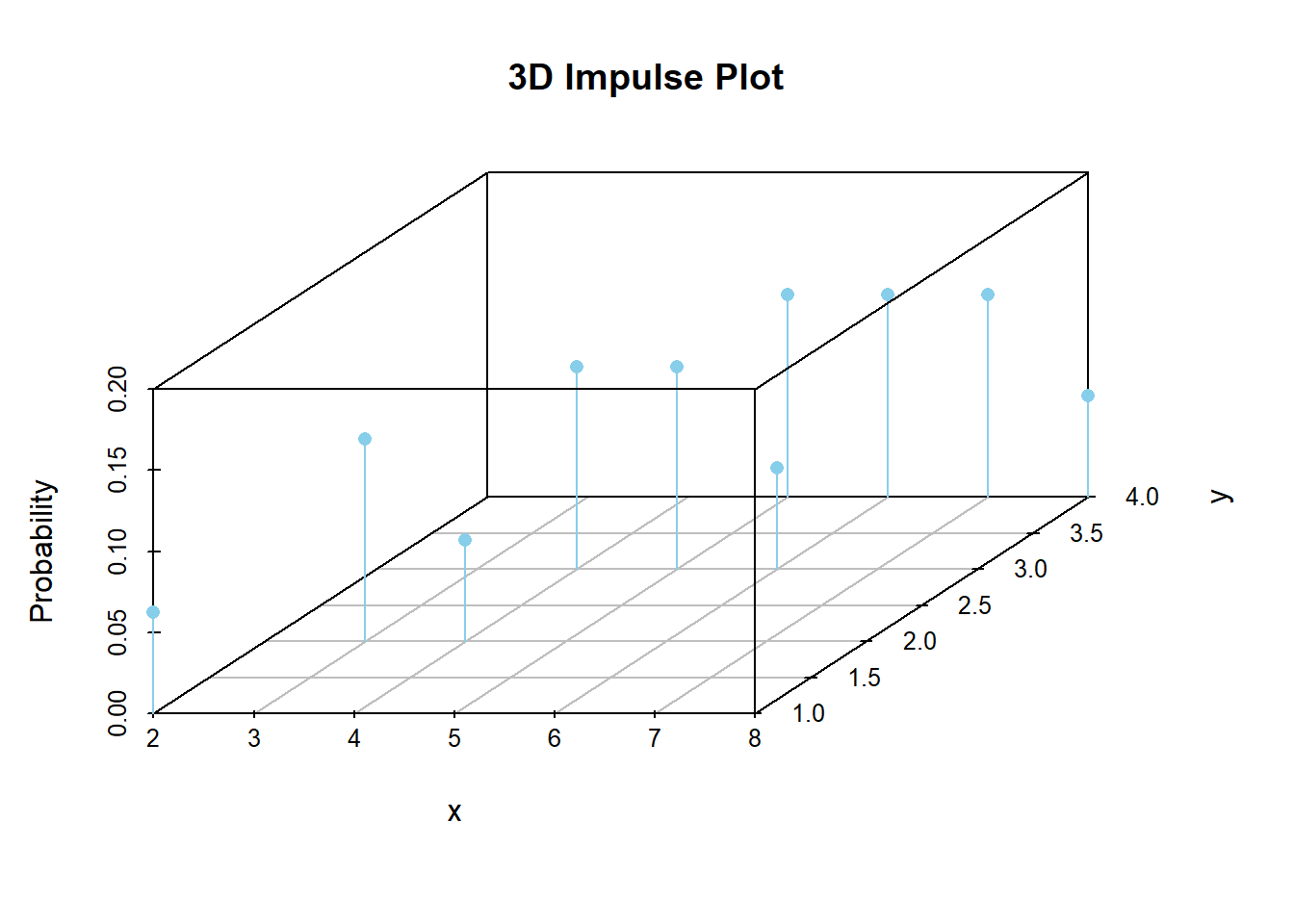
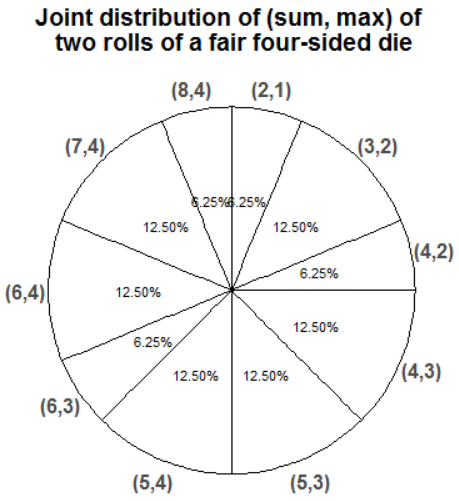
Example 12.2 Continuing the dice rolling example, construct a spinner representing the joint distribution of \(X\) and \(Y\).
- The joint probability mass function (pmf) of two discrete random variables \((X,Y)\) defined on a probability space is the function defined by \[ p_{X,Y}(x,y) = \text{P}(X= x, Y= y) \qquad \text{ for all } x,y \]
- Remember to specify the possible \((x, y)\) pairs when defining a joint pmf.
Example 12.3 Let \(X\) be the number of home runs hit by the home team, and \(Y\) the number of home runs hit by the away team in a randomly selected Major League Baseball game. Suppose that \(X\) and \(Y\) have joint pmf
\[ p_{X, Y}(x, y) = \begin{cases} e^{-2.3}\frac{1.2^{x}1.1^{y}}{x!y!}, & x = 0, 1, 2, \ldots; y = 0, 1, 2, \ldots,\\ 0, & \text{otherwise.} \end{cases} \]
Compute and interpret the probability that the home teams hits 2 home runs and the away team hits 1 home run.
Construct a two-way table representation of the joint pmf (you can use software or a spreadsheet).
Compute and interpret the probability that each team hits at most 3 home runs.
Compute and interpret the probability that both teams combine to hit a total of 3 home runs.
Compute and interpret the probability that the home team and the away team hit the same number of home runs.
Compute and interpret the probability that the home team hits 2 home runs.
Compute and interpret the probability that the away team hits 1 home run.
- Recall that we can obtain marginal distributions from a joint distribution.
- Marginal pmfs are determined by the joint pmf via the law of total probability.
- If we imagine a plot with blocks whose heights represent the joint probabilities, the marginal probability of a particular value of one variable can be obtained by “stacking” all the blocks corresponding to that value.
\[\begin{align*} p_X(x) & = \sum_y p_{X,Y}(x,y) & & \text{a function of $x$ only} \\ p_Y(y) & = \sum_x p_{X,Y}(x,y) & & \text{a function of $y$ only} \\ \end{align*}\]
12.1 Joint probability density fuctions
The joint distribution of two continuous random variables can be specified by a joint pdf, a surface specifying the density of \((x, y)\) pairs.
The probability that the \((X,Y)\) pair of random variables lies is some region is the volume under the joint pdf surface over the region.
The joint probability density function (pdf) of two continuous random variables \((X,Y)\) defined on a probability space is the function \(f_{X,Y}\) which satisfies, for any region \(S\) \[ \text{P}[(X,Y)\in S] = \iint\limits_{S} f_{X,Y}(x,y)\, dx dy \]
A joint pdf is a surface with height \(f_{X,Y}(x,y)\) at \((x, y)\).
The probability that the \((X,Y)\) pair of random variables lies in the region \(A\) is the volume under the pdf surface over the region \(A\)
The height of the density surface at a particular \((x,y)\) pair is related to the probability that \((X, Y)\) takes a value “close to” \((x, y)\): \[ \text{P}(x-\epsilon/2<X < x+\epsilon/2,\; y-\epsilon/2<Y < y+\epsilon/2) = \epsilon^2 f_{X, Y}(x, y) \qquad \text{for small $\epsilon$} \]
The joint distribution is a distribution on \((X, Y)\) pairs. A mathematical expression of a joint distribution is a function of both values of \(X\) and values of \(Y\). Pay special attention to the possible values; the possible values of one variable might be restricted by the value of the other.
The marginal distribution of \(Y\) is a distribution on \(Y\) values only, regardless of the value of \(X\). A mathematical expression of a marginal distribution will have only values of the single variable in it; for example, an expression for the marginal distribution of \(Y\) will only have \(y\) in it (no \(x\), not even in the possible values).
12.2 Independence of random variables
- Two random variables \(X\) and \(Y\) defined on a probability space with probability measure \(\text{P}\) are independent if \(\text{P}(X\le x, Y\le y) = \text{P}(X\le x)\text{P}(Y\le y)\) for all \(x, y\). That is, two random variables are independent if their joint cdf is the product of their marginal cdfs.
- Random variables \(X\) and \(Y\) are independent if and only if the joint distribution factors into the product of the marginal distributions. The definition is in terms of cdfs, but analogous statements are true for pmfs and pdfs. \[\begin{align*} \text{Discrete RVs $X$ and $Y$} & \text{ are independent}\\ \Longleftrightarrow p_{X,Y}(x,y) & = p_X(x)p_Y(y) & & \text{for all $x, y$} \end{align*}\] \[\begin{align*} \text{Continuous RVs $X$ and $Y$} & \text{ are independent}\\ \Longleftrightarrow f_{X,Y}(x,y) & = f_X(x)f_Y(y) & & \text{for all $x,y$} \end{align*}\]
- Random variables \(X\) and \(Y\) are independent if and only if their joint distribution can be factored into the product of a function of values of \(X\) alone and a function of values of \(Y\) alone. That is, \(X\) and \(Y\) are independent if and only if there exist functions \(g\) and \(h\) for which \[ f_{X,Y}(x,y) \propto g(x)h(y) \qquad \text{ for all $x$, $y$} \]
- \(X\) and \(Y\) are independent if and only if the joint distribution factors into a product of the marginal distributions. The above result says that you can determine if that’s true without first finding the marginal distributions.
Example 12.4 Let \(X\) be the number of home runs hit by the home team, and \(Y\) the number of home runs hit by the away team in a randomly selected Major League Baseball game. Suppose that \(X\) and \(Y\) are independent, \(X\) has a Poisson(1.2) distribution and \(Y\) has a Poisson(1.1) distribution.
Find the joint pmf of \(X\) and \(Y\).
How could you have from the setup of Example 12.3 that \(X\) and \(Y\) were independent?